Tracer Transport Operators

To model marine biogeochemical processes on a global scale we need to be able to account for the movement of chemical constituents both horizontally and vertically. We do this with a tracer transport operator. When this operator acts on a tracer field it produces the advective-diffusive divergence of the tracer.

Discretization

In order to represent the transport operator on a computer we have to discretize the tracer concentration field and the operator. Once discretized the tracer field is represented as a vector and the operator is represented as a sparse matrix.

Mathematically, the discretization converts an expression with partial derivatives into a matrix vector product:

where $\mathbf{T}$ is the flux divergence transport matrix and $\boldsymbol{C}$ is the tracer concentration vector.

One can go a long way towards understanding what a tracer transport operator is by playing with a simple box model. We therefore introuce a simple box model before moving on to the Ocean Circulation Inverse Model (OCIM).

The simple box model we consider is embeded in a 2×2×2 "shoebox". It has 5 wet boxes and 3 dry boxes, as illustrated below:

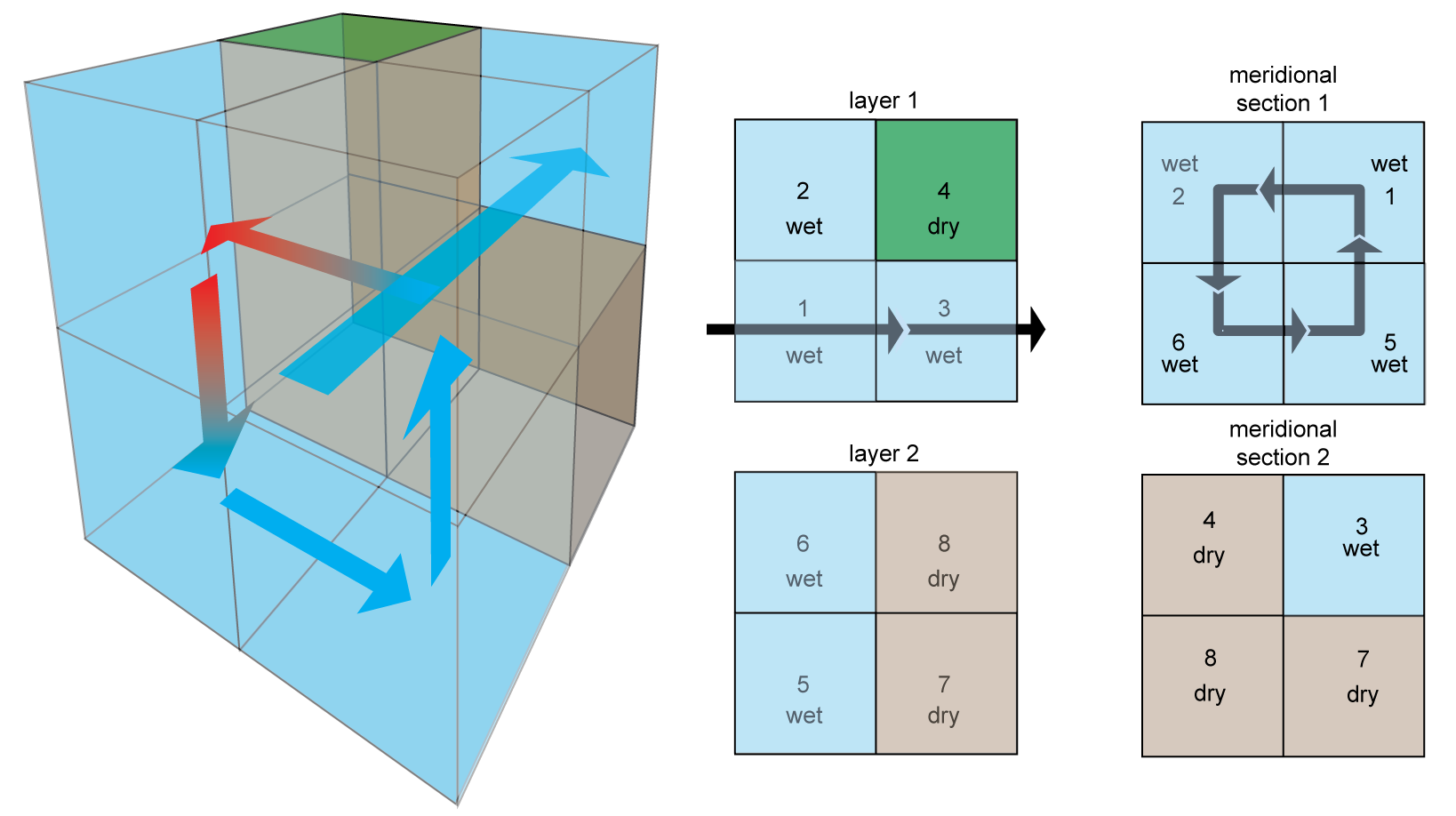
The circulation consists of

• a meridional overturning circulation flowing in a cycle through boxes 1 → 2 → 6 → 5 → 1 (shown in the "meridional section 1" panel above)
• a zonal current in a reentrant cycling through boxes 1 → 3 → 1 (shown in the "layer 1" panel above)
• vertical mixing representing deep convection between boxes 2 ↔ 6 (not shown)

The transport matrix

We start by defining the model boxes, theirs volumes, their indices, and so on:

a = 6367e3   # Earth radius           (m)
A = 4*pi*a^2 # Earth surface area     (m²)
d = 3700     # ocean depth            (m)
V = 0.75*A*d # volume of ocean        (m³)
h = 200      # thickness of top layer (m)

dz = [h*ones(4,1);(d-h)*ones(4,1)] # grid box thicknesses       (m)
dV = (dz/d).*((V/4)*ones(8,1))     # grid box volumes           (m³)
dAz = dV./dz                       # area of face ⟂ to z axis   (m²)
dy = sqrt.(dAz)                    # north-south side length    (m)
dx = sqrt.(dAz)                    # east-west side length      (m)
dAx = dV./dy                       # area of face ⟂ to x axis   (m²)
dAy = dV./dx                       # area of face ⟂ to y axis   (m²)

msk = [1, 1, 1, 0, 1, 1, 0, 0]     # wet-dry mask wet=1 dry = 0
iwet = findall(x -> x == 1, msk)        # index to wet gridboxes
idry = findall(x -> x == 0, msk)        # index to dry gridboxes
srf = [1, 1, 1, 0, 0]              # surface mask srface=1 bottom = 0
isrf = findall(x -> x == 1, srf) ;
iwet

5-element Array{Int64,1}:
 1
 2
 3
 5
 6

As you can see, iwet is the the vector of indices of the wet boxes.

We now create the transport matrix as the flux divergence of the dissolved tracer transport due to the ocean circulation:

using LinearAlgebra
using SparseArrays
TRdiv = spzeros(8,8)
ACC = 100e6  # (m³/s) ACC for Antarctic Circumpoloar Current
TRdiv += sparse([1,1], [1,3], dV[1] \ [ACC, -ACC], 8, 8)
TRdiv += sparse([3,3], [3,1], dV[3] \ [ACC, -ACC], 8, 8)
MOC = 15e6    # (m³/s) MOC for Meridional Overturning Circulation
TRdiv += sparse([1,1], [1,5], dV[1] \ [MOC, -MOC], 8, 8)
TRdiv += sparse([2,2], [2,1], dV[2] \ [MOC, -MOC], 8, 8)
TRdiv += sparse([5,5], [5,6], dV[5] \ [MOC, -MOC], 8, 8)
TRdiv += sparse([6,6], [6,2], dV[6] \ [MOC, -MOC], 8, 8)
MIX = 10e6      # (m³/s) MIX for vertical mixing at high northern latitudes
TRdiv += sparse([2,2], [2,6], dV[2] \ [MIX, -MIX], 8, 8)
TRdiv += sparse([6,6], [6,2], dV[6] \ [MIX, -MIX], 8, 8)
TRdiv = TRdiv[iwet,iwet]
Matrix(TRdiv)

5×5 Array{Float64,2}:
  6.01987e-9   0.0         -5.23467e-9  -7.852e-10     0.0        
 -7.852e-10    1.30867e-9   0.0          0.0          -5.23467e-10
 -5.23467e-9   0.0          5.23467e-9   0.0           0.0        
  0.0          0.0          0.0          4.48686e-11  -4.48686e-11
  0.0         -7.4781e-11   0.0          0.0           7.4781e-11 

Radiocarbon

Radiocarbon, ¹⁴C, is produced by cosmic rays in the lower stratosphere and upper troposphere. It quickly reacts with oxygen to produce ¹⁴CO₂, which is then mixed throughout the troposphere and enters the ocean through air–sea gas exchange. Because the halflife of radiocarbon is only 5730 years a significant amount of decay can occur before the dissolved inorganic radiocarbon (DI¹⁴C) can mix uniformally throughout the ocean. As such the ¹⁴C serves as a tracer label for water that was recently in contact with the atmosphere.

Tracer Equation

Mathematically, the ¹⁴C tracer concentration, denoted $R$ (for Radiocarbon), satisfies the following tracer equation:

where $\Lambda(R_\mathsf{atm} - R)$ represents the air–sea exchanges and $R / \tau$ the radioactive decay rate. ($\tau$ is the radioactive decay timescale.) The discretized tracer is thus given by

where $\mathbf{\Lambda}$ is a diagonal matrix with diagonal elements equal to zero except for surface-layer boxes. We can rearrange this equation as

where $\boldsymbol{s} = \mathbf{\Lambda} \, \boldsymbol{1} \, R_\mathsf{atm}$ effectively acts as a fixed source of Radiocarbon from the atmosphere. (Here we multiply $\boldsymbol{1}$, a vector of 1's, to the scalar value of $R_\mathsf{atm}$ to make sure the matrix $\mathbf{\Lambda}$ is applied to a vector, and not a scalar.)

The matrix $\mathbf{M} = \mathbf{T} + \mathbf{\Lambda} + \mathbf{I} / \tau$ simplifies notation even more:

Translation to Julia Code

We will perform an idealized radiocarbon simulation in our model and use TRdiv, defined earlier, for the transport matrix $\mathbf{T}$. In this model we prescribe the atmospheric concentration, $R_\mathsf{atm}$, to be simply equal to 1. (We do not specify its unit or its specific value because it is not important for determining the age of a water parcel — only the decay rate does.) For the air–sea gas exchange, we use a constant piston velocity $\lambda$ of 50m / 10years.

sec_per_year = 365*24*60*60 # s / yr
λ = 50 / 10sec_per_year     # m / s
Λ = λ / h * Diagonal(srf)

5×5 LinearAlgebra.Diagonal{Float64,Array{Float64,1}}:
 7.92745e-10   ⋅            ⋅            ⋅    ⋅ 
  ⋅           7.92745e-10   ⋅            ⋅    ⋅ 
  ⋅            ⋅           7.92745e-10   ⋅    ⋅ 
  ⋅            ⋅            ⋅           0.0   ⋅ 
  ⋅            ⋅            ⋅            ⋅   0.0

where the diagonal matrix Λ is the discrete version of the air-sea exchange operator, $\mathbf{\Lambda}$. We could make it a sparse matrix via

Λ = λ / h * sparse(Diagonal(srf))

5×5 SparseMatrixCSC{Float64,Int64} with 3 stored entries:
  [1, 1]  =  7.92745e-10
  [2, 2]  =  7.92745e-10
  [3, 3]  =  7.92745e-10

instead, to save some memory allocations.

For the radioactive decay we use a timescale $\tau$ of 5730/log(2) years, which we define via

τ = 5730sec_per_year / log(2)  # s

2.6069684053828802e11

We can now create the matrix $\mathbf{M}$ via

M = TRdiv + Λ + I / τ

5×5 SparseMatrixCSC{Float64,Int64} with 12 stored entries:
  [1, 1]  =  6.81645e-9
  [2, 1]  =  -7.852e-10
  [3, 1]  =  -5.23467e-9
  [2, 2]  =  2.10525e-9
  [5, 2]  =  -7.4781e-11
  [1, 3]  =  -5.23467e-9
  [3, 3]  =  6.03125e-9
  [1, 4]  =  -7.852e-10
  [4, 4]  =  4.87045e-11
  [2, 5]  =  -5.23467e-10
  [4, 5]  =  -4.48686e-11
  [5, 5]  =  7.86168e-11

and the source term $\boldsymbol{s}$ via

s = Λ * ones(5) # air-sea source rate

5-element Array{Float64,1}:
 7.927447995941148e-10
 7.927447995941148e-10
 7.927447995941148e-10
 0.0                  
 0.0                  

(Remember we assumed $R_\mathsf{atm}$ to be equal to 1.)

Time stepping

One way to see how the tracer evolves with time is to time step it. Here we will use a simple Euler-backward scheme. That is, we want to simulate $\boldsymbol{R}(t)$ from time $t = 0$ to time $t = \Delta t$, subject to $\boldsymbol{R}(t = 0) = 1$, using the Euler-backward scheme with $n$ timesteps.

We thus discretize the $(0, \Delta t)$ time span into $n$ time intervals of size $\delta t = \Delta t / n$. We apply the Euler-backward scheme, which gives

Reorganizing the equation to express $\boldsymbol{R}(t_{i+1})$ as a function of the rest, we get

Solving such a linear system is done via the backslash operator, \. Let us define the time-stepping function via

euler_backward_step(R, δt, M, s) = (I + δt * M) \ (R + δt * s)

euler_backward_step (generic function with 1 method)

We write another function to run all the time steps and save

function euler_backward(R₀, ΔT, n, M, s)
    R_hist = [R₀]
    δt = Δt / n
    for i in 1:n
        push!(R_hist, euler_backward_step(R_hist[end], δt, M, s))
    end
    return reduce(hcat, R_hist), 0:δt:Δt
end

euler_backward (generic function with 1 method)

Now let's simulate the evolution of radiocarbon for 7500 years, starting from a concentration of 1 everywhere, via

Δt = 7500 * sec_per_year # 7500 years
R₀ = ones(5)             #
R_hist, t_hist = euler_backward(R₀, Δt, 10000, M, s) # runs the simulation

([1.0 0.9999109246519551 … 0.9396963276609469 0.939696301538129; 1.0 0.9999109315312303 … 0.9522690392436967 0.9522690225386061; … ; 1.0 0.999909282162806 … 0.8345437612863147 0.8345436875489095; 1.0 0.9999092850715807 … 0.9058204452782572 0.90582041830955], 0.0:2.3652e7:2.3652e11)

This should take a few seconds to run. Once it's done, we can plot the evloution of radiocarbon through time via

using PyPlot
clf()
C14age_hist = -log.(R_hist) * τ / sec_per_year
plot(t_hist, C14age_hist')
xlabel("simulation time (years)")
ylabel("¹⁴C age (years)")
legend("box " .* string.(iwet))
title("Simulation of the evolution of ¹⁴C age with Euler-backward time steps")
gcf()

The box model took more than 4000 years to spin up to equilibrium. For a box model that's no big deal because it is not computationally expensive to run the model, but for a big circulation model waiting for the model to spinup is painful. We therefore want a better way to find the equilibrium solution.

Solving Directly for the Steady State

One thing we notice is that when the model is at equilibrium, the $\partial \boldsymbol{R} / \partial t$ term vanishes and the steady state solution is simply given by the solution to the following linear system of equations

which can be solved by directly inverting the $\mathbf{M}$ matrix.

R_final = M \ s

5-element Array{Float64,1}:
 0.9396621017627408
 0.9522471525409573
 0.9469952645219785
 0.8344471511771245
 0.9057851117656104

Converting radiocarbon into years gives the following values

C14age_final = -log.(R_final) * τ / sec_per_year
println.("box ", iwet, ": ", round.(C14age_final), " years");

5-element Array{Nothing,1}:
 nothing
 nothing
 nothing
 nothing
 nothing

These are exactly the limit that the Radiocarbon age reaches after about 4000 years of simulation!

Exercise

Try modifying the strength of the currents of the high latitude convective mixing to see how it affects the ¹⁴C-ages.

This page was generated using Literate.jl.